Express Limit As Definite Integral

Next: About this certificate ...

THE LIMIT DEFINITION OF A DEFINITE INTEGRAL

The following problems involve the limit definition of the definite integral of a continuous part of one variable on a airtight, bounded interval. Begin with a continuous part $y=f(x)$ on the interval $[a, b]$ . Allow

$a=x_{0}, x_{1}, x_{2}, x_{3},$ ... $, x_{n-2}, x_{n-1}, x_{n}=b$

be an arbitrary (randomly selected) partition of the interval $[a, b]$ , which divides the interval into $n$ subintervals (subdivisions). Allow

$c_{1}, c_{2}, c_{3},$ ... $, c_{n-2}, c_{n-1}, c_{n}$

exist the sampling numbers (or sampling points) selected from the subintervals. That is,

$c_{1}$ is in $[x_{0}, x_{1}]$ ,

$c_{2}$ is in $[x_{1}, x_{2}]$ ,

$c_{3}$ is in $[x_{2}, x_{3}]$ , ... ,

$c_{n-2}$ is in $[x_{n-3}, x_{n-2}]$ ,

$c_{n-1}$ is in $[x_{n-2}, x_{n-1}]$ ,

and

$c_{n}$ is in $[x_{n-1}, x_{n}]$ .

Define the mesh of the partition to be the length of the largest subinterval. That is, permit

$\Delta x_{i} = x_{i} - x_{i-1} \ \$

for $i = 1, 2, 3, ..., n$ and define

$mesh = \displaystyle{ \max_{1 \le i \le n} \{ x_{i} - x_{i-1} \}}$ .

The definite integral of $f$ on the interval $[a, b]$ is about by and large defined to exist

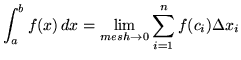$\displaystyle{ \int^{b}_{a} f(x) \, dx} = \displaystyle{ \lim_{mesh \to 0} \sum_{i=1}^{n} f(c_{i}) \Delta x_{i} }$ .

For convenience of computation, a special example of the above definition uses $n$ subintervals of equal length and sampling points chosen to exist the correct-paw endpoints of the subintervals. Thus, each subinterval has length

equation (*) 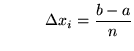$\ \ \ \ \ \ \ \ \Delta x_{i} = \displaystyle{ b-a \over n }$

for $i = 1, 2, 3, ..., n$ and the correct-hand endpoint formula is

equation (**) 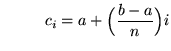$\ \ \ \ \ \ \ \ c_{i} = \displaystyle{ a + \Big( { b-a \over n } \Big) i }$

for $i = 1, 2, 3, ..., n$ . The definite integral of $f$ on the interval $[a, b]$ can now be alternatively defined by

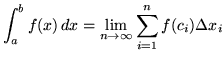$\displaystyle{ \int^{b}_{a} f(x) \, dx} = \displaystyle{ \lim_{n \to \infty} \sum_{i=1}^{n} f(c_{i}) \Delta x_{i} }$ .

Nosotros will need the following well-known summation rules.

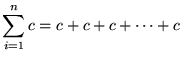$\displaystyle{ \sum_{i=1}^{n} c = c + c + c + \cdots + c }$ (n times) 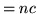$= nc$ , where 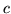$c$ is a abiding
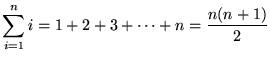
$\displaystyle{ \sum_{i=1}^{n} i = 1 + 2 + 3 + \cdots + n = { n(n+1) \over 2 } }$
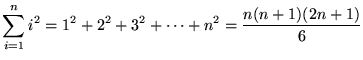
$\displaystyle{ \sum_{i=1}^{n} i^2 = 1^2 + 2^2 + 3^2 + \cdots + n^2 = { n(n+1)(2n+1) \over 6 } }$
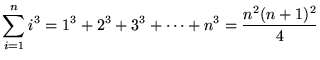
$\displaystyle{ \sum_{i=1}^{n} i^3 = 1^3 + 2^3 + 3^3 + \cdots + n^3 = { n^2(n+1)^2 \over 4 } }$
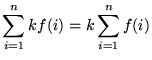$\displaystyle{ \sum_{i=1}^{n} k f(i) } = \displaystyle{ k \sum_{i=1}^{n} f(i) }$ , where 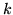$k$ is a constant
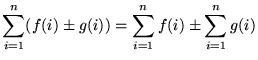
$\displaystyle{ \sum_{i=1}^{n} (f(i) \pm g(i)) } = \displaystyle{ \sum_{i=1}^{n} f(i) \pm \sum_{i=1}^{n} g(i) }$

Nearly of the post-obit problems are boilerplate. A few are somewhat challenging. If you are going to try these problems before looking at the solutions, you tin can avoid common mistakes by using the formulas given above in exactly the course that they are given. Solutions to the first eight problems will apply equal-sized subintervals and right-paw endpoints as sampling points as shown in equations (*) and (**) above.

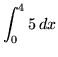PROBLEM 1 : Use the limit definition of definite integral to evaluate $\displaystyle{ \int^{4}_{0} 5 \, dx }$ .

Click Here to run across a detailed solution to trouble 1.
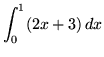Trouble 2 : Use the limit definition of definite integral to evaluate $\displaystyle{ \int^{1}_{0} (2x+3) \, dx }$ .

Click HERE to run into a detailed solution to problem 2.
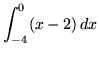Trouble 3 : Employ the limit definition of definite integral to evaluate $\displaystyle{ \int^{0}_{-4} (x-2) \, dx }$ .

Click HERE to meet a detailed solution to trouble 3.
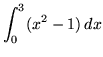Trouble 4 : Apply the limit definition of definite integral to evaluate $\displaystyle{ \int^{3}_{0} (x^2-1) \, dx }$ .

Click HERE to see a detailed solution to problem 4.
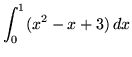PROBLEM v : Employ the limit definition of definite integral to evaluate $\displaystyle{ \int^{1}_{0} (x^2-x+3) \, dx }$ .

Click Here to meet a detailed solution to problem v.
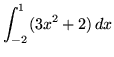PROBLEM 6 : Use the limit definition of definite integral to evaluate $\displaystyle{ \int^{1}_{-2} (3x^2+2) \, dx }$ .

Click Hither to encounter a detailed solution to problem 6.
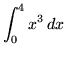Trouble seven : Use the limit definition of definite integral to evaluate $\displaystyle{ \int^{4}_{0} x^3 \, dx }$ .

Click HERE to see a detailed solution to trouble 7.
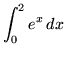Problem 8 : Use the limit definition of definite integral to evaluate $\displaystyle{ \int^{2}_{0} e^x \, dx }$ .

Click Hither to run across a detailed solution to problem 8.
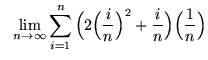Problem 9 : Write the following limit as a definite integral : $\ \ \displaystyle{ \lim_{n \to \infty} \sum_{i=1}^{n} \Big( 2 \Big({i \over n}\Big)^2 + {i \over n} \Big) \Big({1 \over n}\Big) }$ .

Click HERE to see a detailed solution to trouble 9.
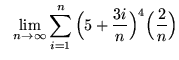Problem 10 : Write the following limit every bit a definite integral : $\ \ \displaystyle{ \lim_{n \to \infty} \sum_{i=1}^{n} \Big( 5 + {3i \over n} \Big)^4 \Big({2 \over n}\Big) }$ .

Click Hither to see a detailed solution to problem 10.
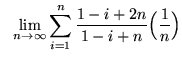PROBLEM xi : Write the following limit as a definite integral : $\ \ \displaystyle{ \lim_{n \to \infty} \sum_{i=1}^{n} { 1-i+2n \over 1-i+n } \Big({1 \over n}\Big) }$ .

Click Hither to see a detailed solution to trouble 11.
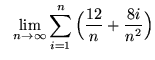PROBLEM 12 : Write the following limit as a definite integral : $\ \ \displaystyle{ \lim_{n \to \infty} \sum_{i=1}^{n} \Big( {12 \over n} + {8i \over n^2} \Big) }$ .

Click HERE to see a detailed solution to problem 12.
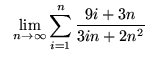PROBLEM thirteen : Write the following limit equally a definite integral : $\ \ \displaystyle{ \lim_{n \to \infty} \sum_{i=1}^{n} { 9i+3n \over 3in+2n^2} }$ .

Click Hither to run across a detailed solution to trouble 13.
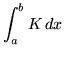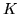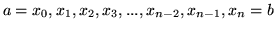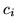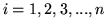Problem fourteen : Use the limit definition of definite integral to evaluate $\displaystyle{ \int^{b}_{a} K \, dx }$ , where $K$ is a constant. Employ an arbitrary partition $a=x_{0}, x_{1}, x_{2}, x_{3}, ... , x_{n-2}, x_{n-1}, x_{n}=b$ and arbitrary sampling numbers $c_{i}$ for $i = 1, 2, 3, ..., n$ .

Click Hither to see a detailed solution to trouble fourteen.
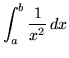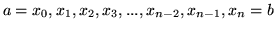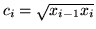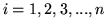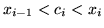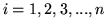Problem 15 : Use the limit definition of definite integral to evaluate $\displaystyle{ \int^{b}_{a} {1 \over x^2} \, dx }$ . Utilise an arbitrary partitioning $a=x_{0}, x_{1}, x_{2}, x_{3}, ... , x_{n-2}, x_{n-1}, x_{n}=b$ and the sampling number $c_{i} = \sqrt{ x_{i-1}x_{i} }$ for $i = 1, 2, 3, ..., n$ . Begin by showing that $x_{i-1} < c_{i} < x_{i}$ for $i = 1, 2, 3, ..., n$ . Presume that $0 < a < b$ .
Click HERE to see a detailed solution to problem xv.